Форма входа |
|---|
Категории раздела | |||||||
|---|---|---|---|---|---|---|---|
|
Поиск |
|---|
Архив записей |
|---|
Статистика |
|---|
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
Сайт
Блог
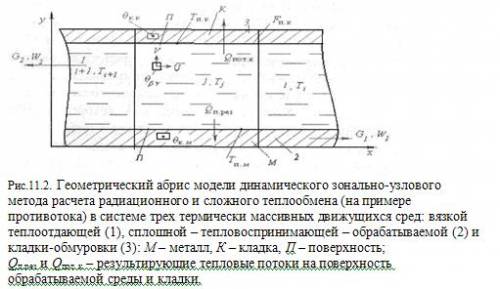
Главная » 2013 Июнь 17 » Л11. Динамический зонально-узловой метод (ДЗУ-метод).20:42 Л11. Динамический зонально-узловой метод (ДЗУ-метод). |
На совреременном этапе решение задач теплообмена применительно к АСУ ТП требует учета как динамики нагрева (как кладки, так и нагреваемого материала), так и учета газодинамики и процессов кондуктивного переноса в газообразной теплопередающей и в тепловоспринимающей среде. Таким образом, с учетом наличия радиационного переноса возникает задача сложного теплообмена, в котором системы уравнений типа (11.1), (11.2)
До последнего времени применительно к реальным объектам управления эта комплексная задача не была решена: отдельно решались уравнения теплообмена и газодинамики, при этом учет динамики нагрева, как правило, не проводился. К настоящему времени разработаны приемы, позволяющие стыковать решения уравнений конечно-разностным методом в рамках крупной сетки (в зональной постановке) для учета процессов радиационного переноса и в рамках мелкой сетки (узлов) для учета процессов кондуктивного переноса и газодинамики. При этом удается учитывать динамику нагрева. В целом этот метод, разработанный под руководством В. Г. Лисиенко, определяется как динамический зонально-узловой метод (ДЗУ-метод) и может в настоящее время являться основой поддерживающей модели процессов нагрева третьего уровня управления. Для решения конкретных задач могут использоваться отдельные элементы метода. В целом метод опирается на следующие основные положения (см. рис.11.2). 1. В основу решения системы (11.2) положен многозональный
подход (метод крупной сетки), связанный с разбиением системы
из движущихся газов и нагреваемых материалов, а также кладки на т объемных
и n поверхностных зон (см. рис.11.2) и записью системы
уравнений теплового баланса и теплопередачи (в записи радиационного
члена через селективные коэффициенты радиационного обмена 
Важнейшей задачей численного решения систем уравнений математической модели на основе ДЗУ-метода является стыковка системы зональных уравнений (11.3) (крупнозональная сетка) с уравнениями переноса энергии в нагреваемом материале и вязкой газообразной среде (см. уравнения (11.4) и (11.7)). В этих средах осуществляется градиентный перенос, и для численного решения уравнения применяются конечно-разностные методы с использованием относительно мелкой (узловой) сетки. Этой стыковки удалось достигнуть усреднением узловых температур и соответственно приведением их к среднезональным Тj для поверхностных и объемных зон (см. формулы (11.6) и (11.8)). 2. Для нагреваемого материала и кладки-обмуровки используется уравнение энергии и теплопроводности в движущейся среде для среды к в форме 
3. Применяется уравнение энергии и для потока несжимаемой вязкой жидкости (газа) - обрабатывающей среды (двумерный случай): 
Как указывалось, для реализации численного решения системы уравнений (11.4) и (11.7) представляются в конечно-разностной (дискретной) форме с применением сравнительно небольших шагов по координатам сетки Δх,Δу и Δz (мелкая или узловая сетки). Стыковка численных решений на зональной (крупной сетке) по системе уравнений (11.3) и на узловой (мелкой сетке) по системам уравнений (11.4) и (11.7) проводится, как уже отмечалось, путем использования усреднений температур (11.6) и (11.8). Для численного решения системы конечно-разностных нелинейных уравнений (11.3) в совокупности с системами уравнений (11.5) и (11.7) могут применяться различные эффективные итерационные методы, обеспечивающие быстродействие и сходимость алгоритмов: комбинированные неявно-явные схемы, метод Ньютона-Рафсона и др. 4. Данная система дополняется уравнениями сохранения массы и движения (уравнением Навье-Стокса) для решения задачи гидродинамики в газовой среде, причем турбулентная вязкость определяется из "К- ε " модели турбулентности. Например, в криволинейных ортогональных координатах (двумерный случай) уравнения неразрывности и гидродинамики имеют вид 
j=2 для i=1 и i=2 . Здесь х - криволинейные координаты; S - площади грани объема, l - коэффициенты Ламе; i и j – индексы компонент. Отметим, что уравнение типа (11.12), по существу, является видоизменённой частью обобщенного уравнения (11.1) с основой на градиентном члене L(Vi). В обобщенной форме подобного типа уравнение используется для ряда переменных φi- (см. таблицу 1) - кроме скорости Vi - для энергии турбулентных пульсаций Кi и их диссипации εi, а также концентрации горючего и окислителя сi,-. В этом случае в рамках данной модели оно используется для вычисления коэффициентов модели турбулентности К и ε, а также для расчетов процессов перемешивания и горения. При этом в такой обобщенной форме в прямоугольных координатах уравнение (11.1) принимает форму, типичную для трехмерных моделей и отражающую основные особенности табл. 1 
где φi - рассматриваемый параметр
(скорость, энергия трубных пульсаций и их диссипаций,
концентрация топлива и окислителей), Г - градиентный параметр
(теплопроводность, динамическая вязкость, коэффициент диффузии);
для гидродинамических явлений при этом В настоящее время реализация ДЗУ-метода и его отдельных элементов доведена до прикладных программ. Как составные части этого метода разработаны дополнительные блоки: алгоритмы и программы. Это экспресс-методы определения обобщенных коэффициентов излучения; двухэтапный метод (Монте-Карло - линейная система) определения разрешающих угловых коэффициентов излучения; 9-, 2- и многополосные модели спектров излучения газов и модели излучения сажистых частиц пламени; определение локальных характеристик; решение внутренней задачи теплопроводности на криволинейной сетке; определение эффективной теплопроводности слоистых материалов и штабелей огнеупоров; оценка рассеяния; расчеты угловых коэффициентов при сложной геометрии; модели выгорания, подсоса и сажевыделения по длине факелов и др. |
|
|
| Всего комментариев: 0 | |