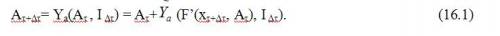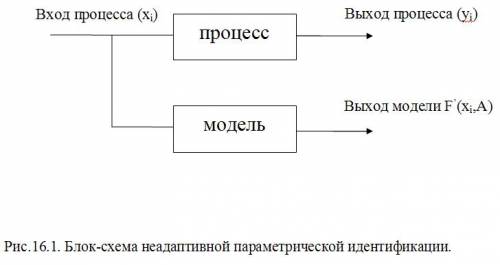
Введем обозначения:

Y – вектор переменных выхода;

U – вектор управляющих воздействий;

X – вектор переменных входа (часть наблюдений, касающихся переменных входа, контролируемые возмущения d₁ по схеме Рея);

A – вектор параметров модели;

         Тогда под параметрической идентификацией понимаем процесс переопределения параметров A в режиме нормальной эксплуатации объекта, при этом структура математической модели известна и выглядит следующим образом St: Y=F (X, U, A).

Неадаптивная параметрическая идентификация

В задаче параметрической идентификации (рис. 16.1) присутствуют два типа данных:

1.     Априорные данные (в виде структуры мат.модели):

St: Y=F (X, U, A)

     Y=F ^| (X, A) |_{u-фиксированное}

                В задаче идентификации, т.к. вход U-вызывающая сила, они не характеризуют механизм (динамику) модели, поэтому U=const

2.     Апостериорные данные (наблюдения):

I=<X_i, Y_i>, i=1..N – число наблюдений,

I – информация о наблюдаемых входах и выходах по N наблюдениям.

Тогда задача параметрической идентификации выглядит следующим образом:

A=Y (St, I), где Y – алгоритм идентификации.

Т.о. необходимо отыскать такой алгоритм определения вектора A, чтобы была минимальна ошибка выходов процесса и модели при реакции на одинаковый вход. Следовательно, эта задача находится в классе минимизационных задач, в которых отыскивается минимум погрешности моделирования по некоторому выбранному заранее критерию качества.

         Неадаптивная идентификация в режиме off-line позволяет получить оптимальные оценки параметров A сразу, используя всю информацию I по N наблюдениям за достаточный отрезок времени. Такой подход возможен при использовании детерминированных динамических моделей.

Адаптивная параметрическая идентификация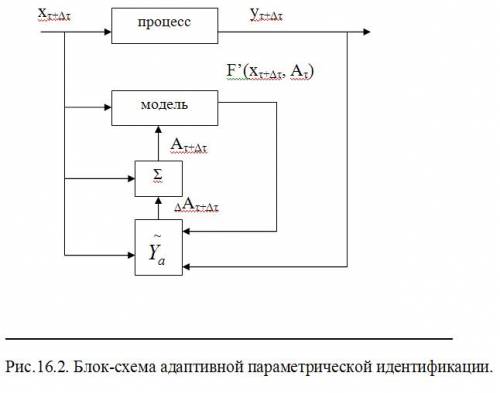

Адаптивная идентификация проводится непрерывно, в режиме on-line. Она представляет собой процесс построения модели объекта в виде аналитической зависимости на основании сведений о значении искомой функции и ее аргументов. В качестве функции может выступать любой искомый обобщенный показатель, а в качестве аргументов - величины координат в пространстве состояний, параметры и показатели. Предполагается, что значения функции определяются значениями ее аргументов. Параметры зависимости функции от своих аргументов находятся автоматически по известным алгоритмам (рис.16.2). Никаких предварительных соображений о структуре зависимости функции от ее аргументов и параметров запаздывания не требуется.

On-line: вектор A_τ= (α₁^τ, …, α_m^τ )^T – параметры модели, определенные на предыдущем шаге по времени τ. На следующем шаге получим I _Δτ=< x_τ+Δτ, y_τ+Δτ> - наблюдения за входом и выходом процесса на текущем шаге по времени τ+Δτ, тогда располагая данными о параметрах A_τ и I _Δτ с помощью адаптивного алгоритма Y_a надо перейти к улучшенным оценкам вектора A на текущем шаге по времени: (A_τ , I _Δτ) –> A_τ+Δτ, тогда сформулируем задачу адаптивной параметрической идентификации.

Т.о. адаптивная идентификация в непрерывном режиме постоянно         корректирует параметры А в целях обеспечения адекватности модели в пределах заданной точности.

       Алгоритм Y_a строится как рекуррентная (непрерывная) процедура,   позволяющая более рационально обеспечивать сходимость алгоритма. Понятно, что адаптивная идентификация необходима при использовании упрощенных (формальных) недетерминированных моделей, у которых природа погрешностей содержится в структуре моделей. В большинстве случаев статических моделей.

Понятие о типовой идентификации.

В классической ТАУ рассматриваются объекты управления как объекты с сосредоточенными параметрами, последние описываются математически через аппарат передаточных функций.

В ТАУ различные элементы систем выделены в класс типовых динамических звеньев.

Тогда становится возможным структурный синтез передаточных функций более сложных объектов. Для этого осуществляют выбор комбинаций динамических звеньев на основе анализа формы входных и выходных сигналов.

Сущность метода  типовой идентификации заключается в том, что на базе накопленного опыта и теоретических исследований в области автоматики по наиболее часто встречающимся характеристикам входных и выходных сигналов выбирается сконструированный заранее оператор (передаточная функция W_{объекта}(p)), близкий к истинному  значению неизвестного оператора объекта.

Т.о., в типовой идентификации проблема удержания модели в состоянии      адекватности нелинейному объекту решается с помощью адаптивных алгоритмов параметрической идентификации.