4.1. Математические модели ОУ и ТП.

Математическая модель (ММ) – это система уравнений (алгебраических, дифференциальных, интегральных, интегро-дифференциальных, линейных и нелинейных), которая достаточно полно отражает наиболее характерные черты и особенности ОУ и ТП в соответствии с целями автоматизированного управления процессом.

Пример линейной математической модели с запаздыванием 2-го порядка:

Модель управления – это математическая модель процесса (объекта), дополненная системой равенств и неравенств, характеризующих критерий оптимальности и условия ограничения.

Пример критериев оптимальности:

Е – расход энергетических ресурсов, Е = min E = E min;

О_к- количество окалин при нагреве металла для целей обработки давлением,       О_к= min О_к;

Р – производительность, Р = Р max;

t – время процесса, t = min t;

Δ – прибыль (для капиталиста), Δ = max Δ, но бывают и ограничения

 Δ  = Δ_норма .

Многокритериальные задачи часто формулируются с помощью комплексного критерия оптимальности:

К_компл = АЕ + ВР + СК_кап = min К_компл     ,      

где Е – расход топлива;

Р – производительность;

К_кап – капитальные затраты;

А,В,С – весовые коэффициенты.

Ограничения.

Ограничения связаны с технологическими характеристиками ОУ и ТП, с требованиями окружающей среды.

Например, если имеется ограничение    Х_вых ≤ Х_вых1 , то из представленного графика (см. рис.6.1.) следует, что и величина оптимального значения 

Х_вых1 < Х_{вых.опт}  при  Х_вх1.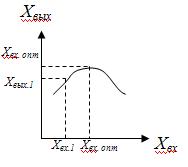

Рис.6.1. Статическая характеристика объекта с экстремумом функции.

Логические модели.

Логические модели – это модели, в которых применяем аппарат логики.

Например, троичная логика        <  =  > - меньше, равно, больше;

                   пятеричная логика    < <      <     =     >     >> - много меньше,                меньше, равно, больше, много больше.

Пример логической таблицы состояний объекта управления:

Рули (входные               Параметры состояния управления

воздействия)

Нечеткая логика.

Вводятся функции принадлежности.

Задается диапазон изменения параметра вместо его точного значения. 

Пример:   1000 ^оС < t < 1500 ^оС

4.2Математические модели, используемые при идентификации, диагностике и управлении.

1.     Эвристические модели. Применяются, когда отсутствуют априорные данные об объектах, оформляются в виде гипотез, предположений. Используются редко.  

2.     Феноменологические модели. Используются следующим образом: закономерности известного объекта применяют для описания неизвестного объекта. Используется метод аналогии – приемы, методика описания ОУ и ТП, при которых различные по своей природе объекты описываются одними и теми же уравнениями.