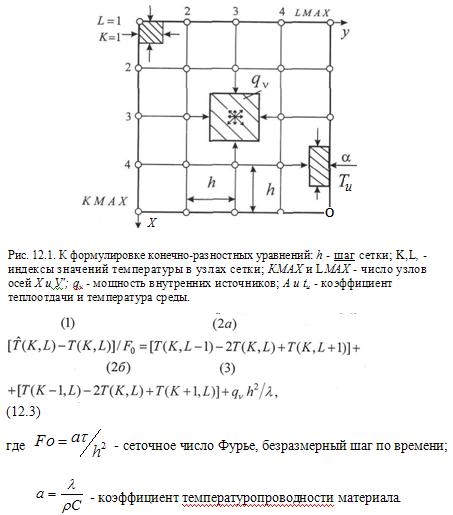
Конечно-разностное представление дифференциального уравнения Фурье и граничных условий сводит решение задачи теплопроводности к расчету температур в конечном числе точек - узлов сетки (рис.12.1). Чтобы дискретизованная задача была близка к исходной, необходимо сделать сетку достаточно частой. Поэтому число неизвестных (т.е. значений температур в узлах) оказывается большим, и решение задачи требует использования ЭВМ. Конечно-разностную аппроксимацию уравнения теплопроводности можно получить, записывая закон сохранения энергии для контрольного объема, содержащего внутренний узел К,L (заштрихован на рис.12.1).

Скорость увеличения внутренней энергии в контрольном объеме определяется соотношением

Отдельные операторы в этом уравнении означают:

(1)  – Скорость увеличения внутренней энергии, конечно-разностная аппроксимация частной производной по времени;

(2а) – подвод теплоты теплопроводностью вдоль оси х, аппроксимация второй производной по х;

(2б) – подвод теплоты вдоль оси у, аппроксимация второй производной по у;

(3)– внутреннее тепловыделение.

Баланс энергии для контрольного объема, содержащего узел на границе области (рис. 12.1), записывается:

Соотношения (12.3) и (12.4) являются приближенными и допускают некоторый произвол при записи правой части. Если все значения температур справа отнесены к исходному моменту времени, то расчетную схему называют явной:

искомое значение температуры T^ в следующий момент времени явно выражается через известные температуры Т в исходный момент времени. Алгоритм расчета оказывается очень простым: начальное условие определяет распределение температур в узлах сетки на старте расчета; затем по (12.3) и (12.4) вычисляют температуру в узлах для следующего момента; процесс повторяется, пока не будет пройден заданный промежуток времени (либо до установления стационарного состояния).

Однако явная схема имеет существенный недостаток: если шаг по времени превышает некоторое критическое значение, в расчете возникают колебания температуры с быстро нарастающей амплитудой. Такое решение не имеет ничего общего с реальным процессом теплопроводности.

Неявная схема получается, если в правых частях уравнений для внутренних и граничных узлов все температуры отнести к последующему моменту времени, т.е. снабдить значками "крышка".

Такая схема абсолютно устойчива, т.е. расчет можно вести с любым шагом по времени, допускаемым    по соображениям точности. Однако теперь, чтобы найти    неизвестную    температуру  ,    необходимо    решить    систему уравнений. Действительно, соотношение (12.3), записанное для каждого внутреннего узла, дает уравнение, содержащее неизвестные температуры в центральном (K,L)    узле   и   четырех   окружающих   узлах.   Объем   вычислений   быстро увеличивается с ростом числа узлов и оказывается недопустимо большим даже для современных ЭВМ.

Метод переменных направлений позволяет сократить объем вычислений по неявной схеме, сохраняя свойство абсолютной устойчивости. Ниже приводится реализация этого метода для областей прямоугольной формы без внутренних источников теплоты.

При построении продольно-поперечной схемы шаг по времени осуществляется, как два полушага: на первом оператор теплопроводности вдоль оси x записывается в неявной форме, а вдоль оси у - в явной; на втором полушаге явным становится первый оператор и неявным - второй. Расчетная схема определяется следующими соотношениями:

Схема переменных направлений является, по-видимому, лучшей для двумерных задач теплопроводности. Ее применение обеспечивает выполнение весьма важного для практических задач требования: получения разумных результатов при расчете на грубых сетках и с большими шагами по времени.