24.1Способ  детерминированной адаптации регулятора

Детерминировано адаптивный регулятор относится к области автоматического регулирования, в частности к системам автоматического регулирования по отклонению с отрицательной обратной связью и может быть использовано в любой отрасли, использующей автоматические регуляторы для целей регулирования параметров состояний объектов управления.

Известен способ адаптации регулятора (корректиров ... Читать дальше »

 23.1Особенности диагностики температурного состояния объекта измерений температуры  при экранировании продуктами сгорания.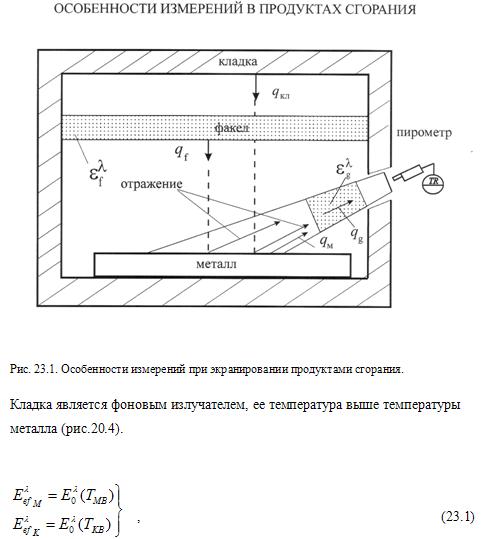

... Читать дальше »

22.1. Физические основы ИК-пирометрии.

Основные законы излучения.

Законы теплового излучения получены применительно к идеальному абсолютно черному телу (АЧТ) и термодинамическому равновесию. Равновесным (черным) излучением называется такое, при котором все тела, входящие в данную излучающую систему, принимают одинаковую температуру. Тепловое излучение носит динамический характер: при одинаковых температурах каждое из тел как ... Читать дальше »

18.1.Определение систем диагностики. Классификация систем диагностики. Их место среди информационных систем и технологий.

... Читать дальше »

Задача параметрической идентификации может быть представлена  следующим образом:

А=J(St, I ... Читать дальше »

Введем обозначения:

Y – вектор переменных выхода;

U – вектор управляющих воздействий;

X – вектор переменных входа (часть наблюдений, касающихся переменных входа, контро ... Читать дальше »

Идентификация математических моделей в СТАУ – методы и способы построения и корректировки математических моделей технологических процессов, объектов управления с использованием метода «черного ящика» на базе эксперимента.

Идентификация процесса – построение математической модели, устанавливающей закономерность между выходными и входными переменными процесса.

Идентификация математических моделей – это методы и способы построения и корректировки математических ... Читать дальше »

 В основе структуры функционирования (блок-схемы) фильтра Калмана-Бьюси заложен алгоритм расширенного фильтра Калмана-Бьюси (для процессов с распределенными параметрами)

... Читать дальше »

... Читать дальше »

14.1. Понятие о фильтре Калмана-Бьюси (ФКБ).

        Как следует из предыдущего, узловым вопросом работоспособности (сходимости) алгоритма оценивания (49) является динамическая настройка «матричного» коэффициента усиления фильтра K(t).

... Читать дальше »

Необходимость постановки задачи оценивания определяется следующими причинами:

Причины класса А:

В реальных технологических процессах, как правило, не удается контролировать все координаты вектора состояния x(t ... Читать дальше »

Конечно-разностное представление дифференциального уравнения Фурье и граничных условий сводит решение задачи теплопроводности к расчету температур в конечном числе точек - узлов сетки (рис.12.1). Чтобы дискретизованная задача была близка к исходной, необходимо сделать сетку достаточно частой. Поэтому число неизвестных (т.е. значений температур в узлах) оказывается большим, и решение задачи требует использования ЭВМ. Конечно-разностную аппроксимацию уравнения теплопроводности можно получить, записывая закон сохран ... Читать дальше »

На совреременном этапе решение задач теплообмена при­менительно к АСУ ТП требует учета как динамики нагрева (как кладки, так и нагреваемого материала), так и учета газо­динамики и процессов кондуктивного переноса в газообраз­ной теплопередающей и в тепловоспринимающей среде. Та­ким образом, с учетом наличия радиационного переноса воз­никает задача сложного теплообмена, в котором системы уравнений типа (11.1), (11.2 ... Читать дальше »

Сущность узлового разбиения и основные изменения, внесенные в расчетную схему метода Монте-Карло, следующие:

1.                Имеющиеся в излучающей системе поверхности задаются алгебраическим уравнением 2-го порядка в общем виде с целью наиболее полного охвата и воспроизведения возможных конфигураций моделируемых объектов.

... Читать дальше »

Как отмечалось ранее, обобщенный термодинамический подход основан на применении первого и второго законов термодинамики. 

1.     Первый закон термодинамики:

... Читать дальше »

        Исключительно стохастические подходы к построению полных математических моделей объектов с распределенными параметрами являются в значительной степени еще менее реалистичными, чем такие же подходы для объектов с сосредоточенными параметрами вследствие значительно большей сложности объектов с распределенными параметрами.

        Поэтому на стадии создания топологии и структуры математической модели необходим детерминированный подход с последующими процедурами параметрической идентификации (адаптация модели) на базе натурных экспериментов. При этом требования к математической модели должны быть такими, чтоб ... Читать дальше »

7.1. Обобщенный термодинамический подход (ОТП) как основа для построения математических моделей.

Математические модели делятся на детерминированные, стохастические и комбинированные:

... Читать дальше »

В последнее время возможности ЭВМ существенно расширились. Это позволяет ставить задачи развития имитационно-оптимизирующего уровня управления, в результате чего и формируется структура, так называемых, (по предложению В.Г, Лисиенко) трехуровневых систем управления технологическими процессами ТАСУ ТП.

           Основные принципы построения трехуровневых АСУ ТП (ТАСУ ТП) основаны, с одной стороны, на тенденции развития интеллектуального уровня современных АСУ ТП, а с другой – на ... Читать дальше »

5.1 Метод аналогии

Метод аналогии – это приемы описания объекта управления и технологического процесса, при которых различные по своей природе объекты описываются одинаковыми уравнениями.

Примеры явлений аналогии проведем с использованием градиентных моделей: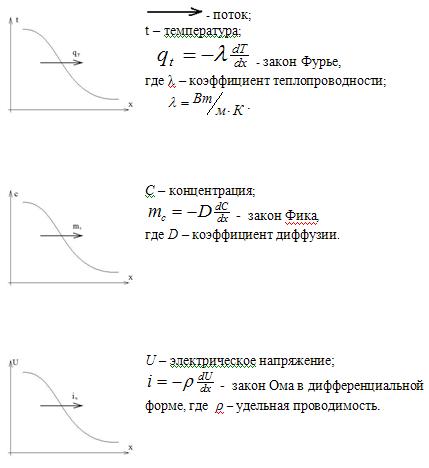

... Читать дальше »

4.1. Математические модели ОУ и ТП.

Математическая модель (ММ) – это система уравнений (алгебраических, дифференциальных, интегральных, интегро-дифференциальных, линейных и нелинейных), которая достаточно полно отражает наиболее характерные черты и особенности ОУ и ТП в соответствии с целями автоматизированного управления процессом.

Пример линейной математической модели с запаздыванием 2-го порядка:

... Читать дальше »

Рис. 3.1. Схема современной АСУ ТП (схема Рея)

Процесс (диагностируемый и управляемый).

Величины на входе (рис.3.1):

... Читать дальше »

Рассмотрим структуру локальной системы автоматического регулирования (рис.2.1).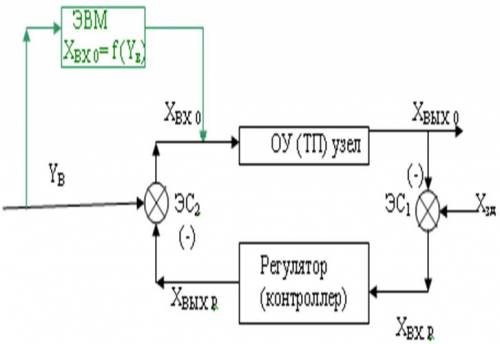

Рис.2.1. Структура локальной системы автоматического регулирования (ЛСАР):

ЭС₁ – элемент сравнения (сравнивает выходную величину Х_{ВЫХ. 0}  с величиной Х_ЗД, вырабатывая значение  Х_{ВХ. Р} = Х_{ВЫХ. 0} - Х_зд);

ЭС₂ – второй элем ... Читать дальше »

1.1. Некоторые даты и временные интервалы.                                               

1930-1960 гг. – ускоренное развитие ЛСАР (локальных систем автоматического регулирования).

... Читать дальше »